树

  • *树－通用目的的树形结构。

  • *二叉树－一种节点最多有两个孩子节点的树形结构。

  • 二叉搜索树(BST)－以某种方式组织自己的节点的二叉树，以求较快的查询速度。

  • *红黑树 - 自平衡二叉搜索树

  • *AVL 树－一种通过旋转来维持平衡的二叉搜索树。

  • *堆－存储在一维数组中的二叉树，所以它不需要使用指针。很适合做为优先队列使用。

  • *字典树 - 一种特殊类型的树结构用来保存关联数据的结构

  • *B 树 - 自平衡搜索树，每个节点可以超过两个子节点

AVL树(AVL Tree)

AVL树是二叉搜索树的自平衡形式，其中子树的高度最多只相差1。

当二叉树的左右子树包含大致相同数量的节点时，称树是 平衡的。 这就是使树搜索速度非常快的原因。 但是如果二元搜索树不平衡，搜索会变得非常慢。

这是一个不平衡树的例子：

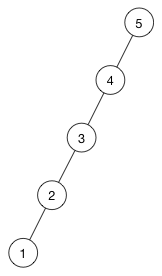
Unbalanced tree

 

所有的子节点都在左侧分支，没有一个在右侧分支。 这与链表基本相同。 因此，搜索需要 O(n) 时间，而不是您期望从二叉搜索树获得的更快的 O(log n) 。

该树的平衡版本如下所示：

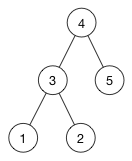
Balanced tree

使二进制搜索树平衡的一种方法是以完全随机的顺序插入节点。 但这并不能保证成功，也不总是切实可行。

另一种解决方案是使用自平衡二叉树。 插入或删除节点后，此类型的数据结构会调整树以使其保持平衡。 这种树的高度保证为 log(n)，其中 n 是节点的数量。 在平衡树上，所有插入，移除和搜索操作仅需 O(logn) 时间。 这意味着快速。;-)

 

介绍AVL树

AVL树通过向左或向右“旋转”树来修复任何不平衡。

如果AVL树中的节点在“高度”上的差异最大为1，则认为它是平衡的。如果树的所有节点都是平衡的，则树本身是平衡的。

节点的height是获取该节点最低叶子所需的步数。 例如，在下面的树中，从A到E需要三个步，因此A的高度为3。B的高度为2，C的高度为1，其他的高度为0，因为它们是叶节点。

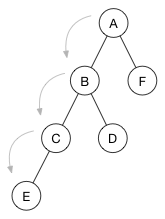
Node height

 

如上所述，在AVL树中，如果节点的左右子树具有相同的高度，则节点是平衡的。 当然不必是完全相同的高度，但差异不能大于1。这些都是平衡树的例子：

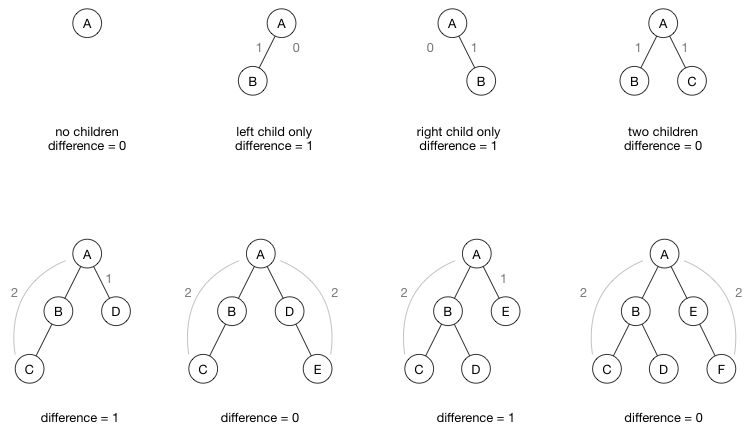
Balanced trees

以下是不平衡的树，因为左子树的高度与右子树相比太大了：

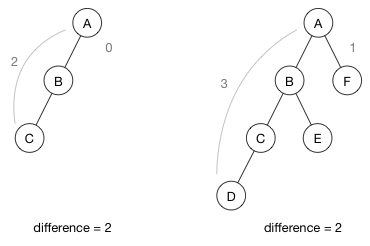
Unbalanced trees

左右子树的高度之间的差异称为平衡因子(balance factor)。 计算方法如下：

balance factor = abs(height(left subtree) - height(right subtree))

如果在插入或删除后平衡因子变得大于1，那么我们需要重新平衡AVL树的这一部分。 这是通过旋转完成的。

译注： abs是绝对值的意思。

 

旋转

每个树节点在变量中跟踪其当前平衡因子。 插入新节点后，我们需要更新其父节点的平衡因子。 如果该平衡因子大于1，我们“旋转”该树的一部分以恢复平衡。

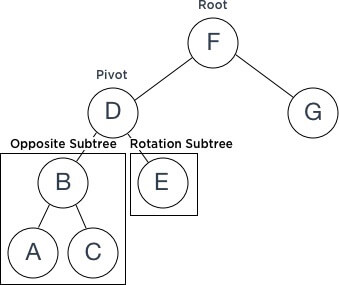
Rotation0

 

对于旋转，我们使用术语：

  • Root - 将要旋转的子树的父节点;

  • Pivot - 旋转后将成为父节点（基本上位于* Root *位置）的节点;

  • RotationSubtree - 旋转侧的Pivot的子树

  • OppositeSubtree - 与旋转侧相对的Pivot的子树

 

让我们举一个使用右（顺时针方向）旋转来平衡不平衡树的示例：

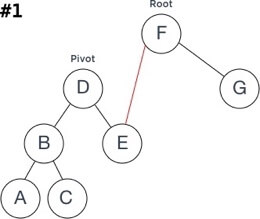
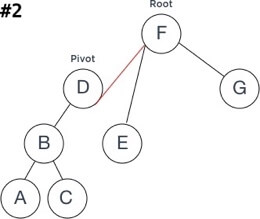
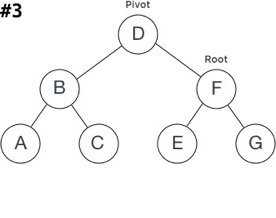
Rotation1 Rotation2 Rotation3

 

旋转步骤可以通过以下方式描述：

  1. 将RotationSubtree指定为Root的新OppositeSubtree;

  2. 将Root指定为Pivot的新RotationSubtree;

  3. 检查最终结果

用伪代码，上面的算法可以写成如下：

Root.OS = Pivot.RS
Pivot.RS = Root
Root = Pivot

 

这是一个恒定时间操作 - O(1) 插入永远不需要超过2次旋转。 删除可能需要最多 log(n) 轮换。

 

代码

 

AVLTree.swift中的大多数代码只是常规二叉搜索树的东西。 您可以在二叉搜索树找到大部分实现。 例如，搜索树是完全相同的。 AVL树唯一不同的是插入和删除节点。

注意： 如果你对二叉搜索树的常规操作有点模糊，我建议你看这边。 这会使AVL树更容易理解。

有趣的位在balance()方法中，在插入或删除节点后调用。

 

扩展阅读

AVL树的维基百科

AVL树是第一个自平衡二叉树。 最近，红黑树似乎更受欢迎。

堆(Heap)

这个话题已经有个辅导文章

 

堆是数组内的二叉树，因此它不使用父/子指针。 堆基于“堆属性”进行排序，“堆属性”确定树中节点的顺序。

 

堆的一般用途：

  • 构建优先队列。

  • 支持堆排序。

  • 快速计算集合中最大（或最小）值。

  • 给你的非程序员朋友留下深刻影响。

 

堆属性

 

有两种堆：max-heap 和 min-heap，它们存储树节点的顺序不同。

 

在max-heap中，每个父节点的值大于其子节点。 在min-heap中，每个父节点的值都小于其子节点。 这称为“堆属性”，对于树中的每个节点都是如此。

一个例子：

A max-heap

 

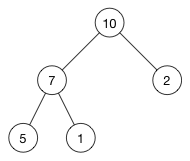
这是一个max-heap，因为每个父节点都大于其子节点。 (10)大于(7)和(2)。 (7)大于(5)和(1)。

堆属性的结果是，max-heap始终将其最大项存储在树的根节点中。 对于min-heap，根节点始终是树中的最小项。 堆属性很有用，因为堆通常用作优先队列来快速访问“最重要的”（译注：最大或最小）元素。

注意： 堆的根节点是最大或最小元素，但其他元素的排序顺序是不可预测的。例如，最大元素始终位于max-heap中的索引0处，但最小元素不一定是最后一个元素。 —— 唯一的保证是，最小元素是叶节点之一，但不知道是哪一个。

 

堆与常规树对比

堆不是二叉搜索树的替代品，它们之间存在相似之处和不同之处。 以下是一些主要差异：

 

节点的顺序。在二叉搜索树（BST）中，左子节点必须小于其父节点，右子节点必须更大。 堆不是这样。 在max-heap中，两个子节点必须小于父节点，而在min-heap中，子节点必须大于父节点。

内存。传统的树比它们存储的数据占用更多的内存。 需要为节点对象和指向左/右子节点的指针分配额外的存储空间。 堆只使用普通数组进行存储，不使用指针。

平衡。 二叉搜索树（BST）必须“平衡”，以便大多数操作具有O(log n)性能。 您可以按随机顺序插入和删除数据，也可以使用AVL树或红黑树，但 我们实际上并不需要对整个树进行排序。 我们只是希望实现堆属性，因此平衡不是问题。 由于堆的结构方式，堆可以保证 O(log n) 的性能。

搜索。 虽然在二叉树中搜索速度很快，但在堆中搜索速度很慢。 搜索不是堆中的最高优先级，因为堆的目的是将最大（或最小）节点放在前面并允许相对快速的插入和删除。

 

数组中的树

用数组实现树状结构似乎比较奇怪，但它在时间和空间上都很高效的。

上面例子中的树用数组存储为：

[ 10, 7, 2, 5, 1 ]

这里的所有了！ 我们不需要比这个简单数组更多的存储空间了。

那么，如果不允许使用任何指针，我们如何知道哪些节点是父节点，哪些节点是子节点？ 好问题！树节点的数组索引与其父节点和子节点的数组索引之间存在明确定义的关系。

如果i是节点的索引，则以下公式给出其父节点和子节点的数组索引：

parent(i) = floor((i - 1)/2)
left(i)   = 2i + 1
right(i)  = 2i + 2

注意right(i)只是left(i)+ 1。 左侧和右侧子节点始终紧挨着存储。

对上面的例子使用这些公式。 填写数组索引，我们应该得到数组中父节点和子节点的位置：

节点数组中的索引(i)父节点索引左子节点索引右子节点索引
100-112
71034
22056
53178
141910

验证这些数组索引确实对应于上面树的图片。

注意： 根节点(10)没有父节点，因为-1不是有效的数组索引。 同样，节点(2)，(5)和(1)没有子节点，因为那些索引大于数组大小，所以用它们之前我们总是要确保我们计算的索引实际上是有效的。

 

回想一下，在max-heap中，父节点的值总是大于（或等于）其子节点的值。 这意味着对于所有数组索引i必须满足以下条件：

array[parent(i)] >= array[i]

验证此堆属性是否适用于示例堆中的数组。

如您所见，这些等式允许我们在不需要指针的情况下找到任何节点的父索引或子索引。 这样消除了使用指针的复杂，这是一种权衡：我们节省了内存空间，但需要额外的计算。 幸运的是，计算速度很快，只需要 O(1) 时间。

理解树中数组索引和位置之间的这种关系很重要。 下面?是一个更大的堆，有15个节点分为四个级别：

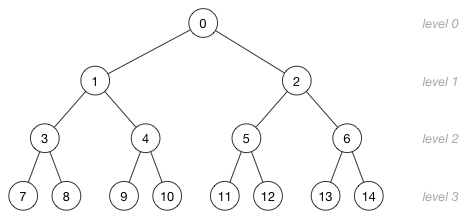
Large heap

 

此图片中的数字不是节点的值，而是存储节点的数组索引！ 下面?是数组索引对应树的不同级别：

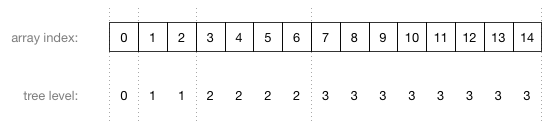
The heap array

要使公式起作用，父节点必须出现在数组中的子节点之前。 你可以在上面的图片中看到。

请注意，此方案有局限性。 您可以使用常规二叉树执行以下操作，但不能使用堆执行以下操作：

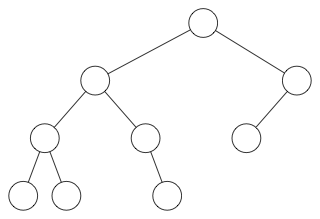
Impossible with a heap

 

除非当前最低级别已满，否则无法开启新级别，因此堆总是具有这种形状：

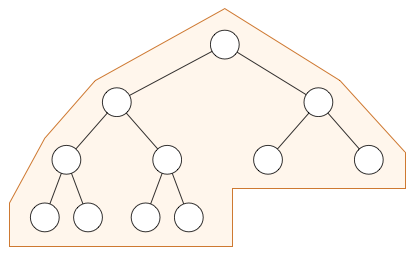
The shape of a heap

注意： 您可以使用堆模拟常规二叉树，但这会浪费空间，您需要将一些数组索引标记为空。

 

突击测验！ 假设我们有数组：

[ 10, 14, 25, 33, 81, 82, 99 ]

这是一个有效的堆吗？ 答案是肯定的！ 从低到高的排序数组是有效的min-heap。 我们可以按如下方式绘制这个堆：

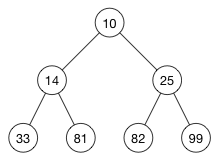
A sorted array is a valid heap

 

堆属性适用于每个节点，因为父节点始终小于其子节点。 （自己验证从高到低排序的数组始终是有效的max-heap。）

注意：但并非每个min-heap都必须是一个排序数组！ 排序数组只是一种特殊情况。 要将堆重新转换为已排序的数组，需要使用堆排序。

 

更多数学！

如果你很好奇，这里有一些描述堆的某些属性的公式。 你不需要知道这些，但它们有时会派上用场。 可以跳过此部分！

树的height定义为从根节点到最低叶节点所需的步数，或者更正式：height是节点之间的最大边数。 高度h的堆具有h + 1级别。

这个堆的高度为3，所以它有4个级别：

Large heap

 

具有n个节点的堆具有高度h = floor(log2(n))。 这是因为我们总是在添加新级别之前完全填满最低级别。 该示例有15个节点，因此高度为 floor(log2(15)) = floor(3.91) = 3。

如果最低级别已满，则该级别包含 2h 个节点。 它上面的树的其余部分包含 2h - 1 个节点。 上面示例就是：最低级别有8个节点，实际上是 2^3 = 8 。 前三个级别包含总共7个节点，即2^3 - 1 = 8 - 1 = 7。

 

因此，整个堆中的节点总数n 为 2^(h+1) - 1。 在示例中，2^4 - 1 = 16 - 1 = 15。

在n个元素堆中，高度为h的最多有 ceil(n/2^(h+1)) 个的节点。（译注：示例中h为0时，ceil(15/2^(0+1)) = 8，h为1时,ceil(15/2^(1+1)) = 4）

叶节点总是位于数组索引 floor(n/2) 到 n-1。(译注： 7 ~ 14) 我们将利用这一事实从数组中快速构建堆。 如果您不相信，请验证此示例。;-)

只是一些数学就能照亮你的一天。☀️

 

你能用堆做什么？

 

在插入或删除元素之后，有两个必要的原始操作来确保堆是有效的max-heap或min-heap：

  • shiftUp()：如果元素比其父元素更大（max-heap）或更小（min-heap），则需要与父元素交换， 这使元素向上移动。

  • shiftDown()。 如果元素比子元素小（max-heap）或更大（min-heap），这个操作使元素向下移动，也称为“堆化(heapify)”。

向上或向下移动是一个递归过程，需要O(log n)时间。

 

以下是基于原始操作的其他操作：

  • insert(value)：将新元素添加到堆的末尾，然后使用shiftUp()来修复堆。

  • remove()：删除并返回最大值(max-heap）或最小值(min-heap）。为了填充元素删除后留下的位置，让最后一个元素移动到根位置，然后使用shiftDown()修复堆。 (有时称为“提取最小值”或“提取最大值”。）

  • removeAtIndex(index)：类似remove()，不仅可以删除根节点，也可以从堆中删除任何节点。如果新元素与其子元素不规整，则调用shiftDown();如果元素与其父元素不规整，则调用shiftUp()。

  • replace(index, value)：为节点分配一个较小(min-heap）或较大(max-heap）的值。因为这会使堆属性失效，所以它使用shiftUp()来修复。 (也称为“减少键”和“增加键”。）

 

以上所有操作都需要时间O(log n)因为向上或向下移动是昂贵的。还有一些操作需要更多时间：

  • search(value)。堆不是为高效搜索而构建的，但replace()和removeAtIndex()操作需要节点的数组索引，因此您需要找到该索引。时间：O(n)。

  • buildHeap(array)：通过重复调用insert()将数组(未排序的）转换为堆。如果您对此很聪明，可以在O(n)时间内完成。

  • 堆排序。由于堆是一个数组，我们可以使用它的唯一属性将数组从低到高排序。时间：O(n lg n)。

堆还有一个peek()函数，它返回最大(max-heap）或最小(min-heap）元素，而不从堆中删除它。时间：O(1)。

 

注意： 到目前为止，您将使用堆执行的最常见操作是使用insert()插入新值，并使用remove()删除最大值或最小值。 两者都需要O(log n)时间。 其他操作用来支持更高级的使用，例如构建优先队列，其中项目的“重要性”在添加到队列后可以改变。

 

向堆中插入元素

 

我们来看一个插入示例，详细了解其工作原理。 我们将值16插入此堆：

The heap before insertion

 

这个堆的数组是[10, 7, 2, 5, 1]。

插入新项目的第一步是将其附加到数组的末尾。 该数组变为：

[ 10, 7, 2, 5, 1, 16 ]

树结构如下：

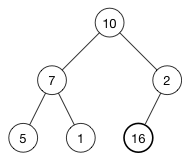
The heap before insertion

(16)被添加到最后一行的第一个可用空间。

不幸的是，堆属性不再满足，因为(2)高于(16)，我们希望更高的数字高于低的数字。 (这是max-heap。)

要恢复堆属性，我们交换(16)和(2)。

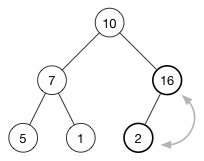
The heap before insertion

 

我们还没有完成，因为(10)也小于(16)。 我们继续将其插入值与其父项交换，直到父项更大或到达树的顶部。 这称为shift-up 或 sifting ，并在每次插入后完成。 它会使一个太大或太小的数字“浮起”树。

 

最后，我们得到：

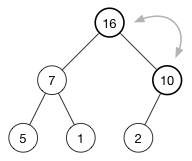
The heap before insertion

 

现在每个父节点都比其子节点更大了。

上移所需的时间与树的高度成正比，需要O(log n)时间。（将节点附加到数组末尾所需的时间仅为O(1)，因此不会降低它的速度。）

 

删除根节点

从树中移除(10)：

The heap before removal

顶部的空白怎么办？

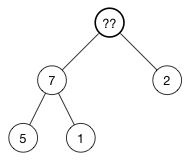
The root is gone

 

插入时，我们将新值放在数组的末尾。 在这里，我们做相反的事情：我们采用我们拥有的最后一个对象，将其直接移动到树的顶部，然后恢复堆属性。

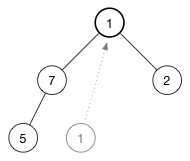
The last node goes to the root

 

让我们来看看如何shift-down(1)。 要维护此max-heap的堆属性，我们希望顶部为最大数。 我们有两个交换位置的候选者：(7)和(2)。 选择这三个节点之间的最高数字位于顶部，那是(7)，所以交换(1)和(7)，得到下面?的树：

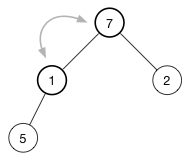
The last node goes to the root

 

继续向下移动，直到节点没有任何子节点，或者它比两个子节点都大。 对于这个堆，只需要一个交换来恢复堆属性：

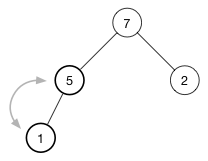
The last node goes to the root

 

完全向下移动所需的时间与树的高度成正比，这需要O(log n)时间。

注意： shiftUp()和shiftDown()一次只能修复一个异常元素。 如果错误的位置有多个元素，则需要为每个元素调用一次这些函数。

 

删除任意节点

 

绝大多数情况下，将删除的是堆根节点，因为这是堆设计的目的。

 

但是，删除任意元素可能很有用。 这是remove()的一般版本，可能涉及shiftDown()或shiftUp()。

让我们再次采用前面的示例树，删除(7)：

The heap before removal

提醒一下，数组是：

[ 10, 7, 2, 5, 1 ]

如您所知，删除元素可能会使max-heap或min-heap属性失效。 要解决这个问题，我们将要移除的节点与最后一个元素交换：

[ 10, 1, 2, 5, 7 ]

最后一个元素是我们将返回的元素; 我们将调用removeLast()将其从堆中删除。 (1)现在是乱序的，因为它小于它的子节点，(5)是在树中应该更高。 我们调用shiftDown()来修复它。

 

但是，向下移动并不是我们需要处理的唯一情况。 也可能发生新元素必须向上移动。 考虑如果从以下堆中删除(5)会发生什么：

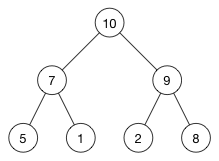
We need to shift up

译注：这个的树对应的数组是[10, 7, 9, 5, 1, 2, 8]。

现在(5)与(8)交换。 因为(8)比它的父节点((7))大，我们需要调用shiftUp()。

 

用数组创建堆

 

将数组转换为堆可以很方便。 只是对数组元素进行洗牌，直到满足堆属性。

在代码中它看起来像这样：

  private mutating func buildHeap(fromArray array: [T]) {
    for value in array {
      insert(value)
    }
  }

 

我们只要为数组中的每个值调用insert()。 简单但不是很高效。 这总共需要O(n log n)时间，因为有n个元素，每个插入需要log n时间。

如果你没有跳过前面数学部分，你已经看到，对于任何堆，数组索引n / 2到n-1的元素都是树的叶节点。 我们可以简单地跳过那些叶子。 我们只需要处理其他节点，因为它们是有一个或多个子节点的父节点，因此可能是错误的顺序。

代码:

  private mutating func buildHeap(fromArray array: [T]) {
    elements = array
    for i in stride(from: (nodes.count/2-1), through: 0, by: -1) {
      shiftDown(index: i, heapSize: elements.count)
    }
  }

 

这里，elements是堆自己的数组。 我们从第一个非叶节点开始向后遍历这个数组，并调用shiftDown()。 这个简单的循环以正确的顺序放置这些节点以及我们跳过的叶节点。 这被称为Floyd算法，只需要O(n)时间。 ✌️

 

搜索堆

 

堆不能用于快速搜索，但如果要使用removeAtIndex()删除任意元素或使用replace()更改元素的值，则需要获取该元素的索引。搜索堆速度很慢。

 

在二叉搜索树中，根据节点的顺序，可以保证快速搜索。 由于堆以不同方式对其节点进行排序，因此二叉搜索不起作用，您需要检查树中的每个节点。

再给出上面堆示例：

The heap

 

如果我们想要搜索节点(1)的索引，我们可以通过线性搜索分步搜索数组[10, 7, 2, 5, 1]。

即使堆属性没有考虑到搜索，我们仍然可以利用它。 我们知道在max-heap中父节点总是比它的子节点大，所以如果父节点已经小于我们要查找的值，我们可以忽略那些子节点(及其子节点等等）。

假设我们想要查看堆是否包含值8(没有包含)。 我们从根(10)开始。 这不是我们想要的，所以我们递归地看看它的左右子节点。 左边的孩子是(7)。 这也不是我们想要的，但由于这是一个max-heap，我们知道查看(7)的子节点是没有意义的，它们总是小于7，因此左侧不会找到8。 同样，对于右节点，(2)，也找不到。

尽管有一点优化，搜索仍然是O(n)操作。

 

注意： 有一种方法可以通过保留一个将节点值映射到索引的附加字典来将查找转换为O(1)操作。 如果你经常需要调用replace()来改变构建在堆上的优先队列中对象的“优先级”，这可能是值得做的。

 

代码

 

有关用Swift代码实现，请参见Heap.swift。 大多数代码都很简单。 唯一棘手的是shiftUp()和shiftDown()。

您已经知道有两种类型的堆：max-heap和min-heap。 它们之间的唯一区别在于它们如何对节点进行排序：首先是最大值或最小值。

不是创建两个不同的版本，MaxHeap和MinHeap，而只有一个Heap对象，它需要一个isOrderedBefore闭包。 此闭包包含确定两个值的顺序的逻辑。 你之前可能已经看过了，因为它也是Swift的sort()的工作原理。

 

要创建一个max-heap整数堆：

var maxHeap = Heap<Int>(sort: >)

要创建一个min-heap整数堆：

var minHeap = Heap<Int>(sort: <)

I just wanted to point this out, because where most heap implementations use the < and > operators to compare values, this one uses the isOrderedBefore() closure.
我只想指出这一点，因为大多数堆实现使用<和>运算符来比较值，这个使用isOrderedBefore()闭包。

扩展阅读

Heap的维基百科

 

字典树（Trie）

这个话题已经有个辅导文章

什么是字典树

Trie（在一些其他实现中也称为前缀树或基数树）是用于存储关联数据结构的特殊类型的树。 Trie作为一个字典可能如下所示：

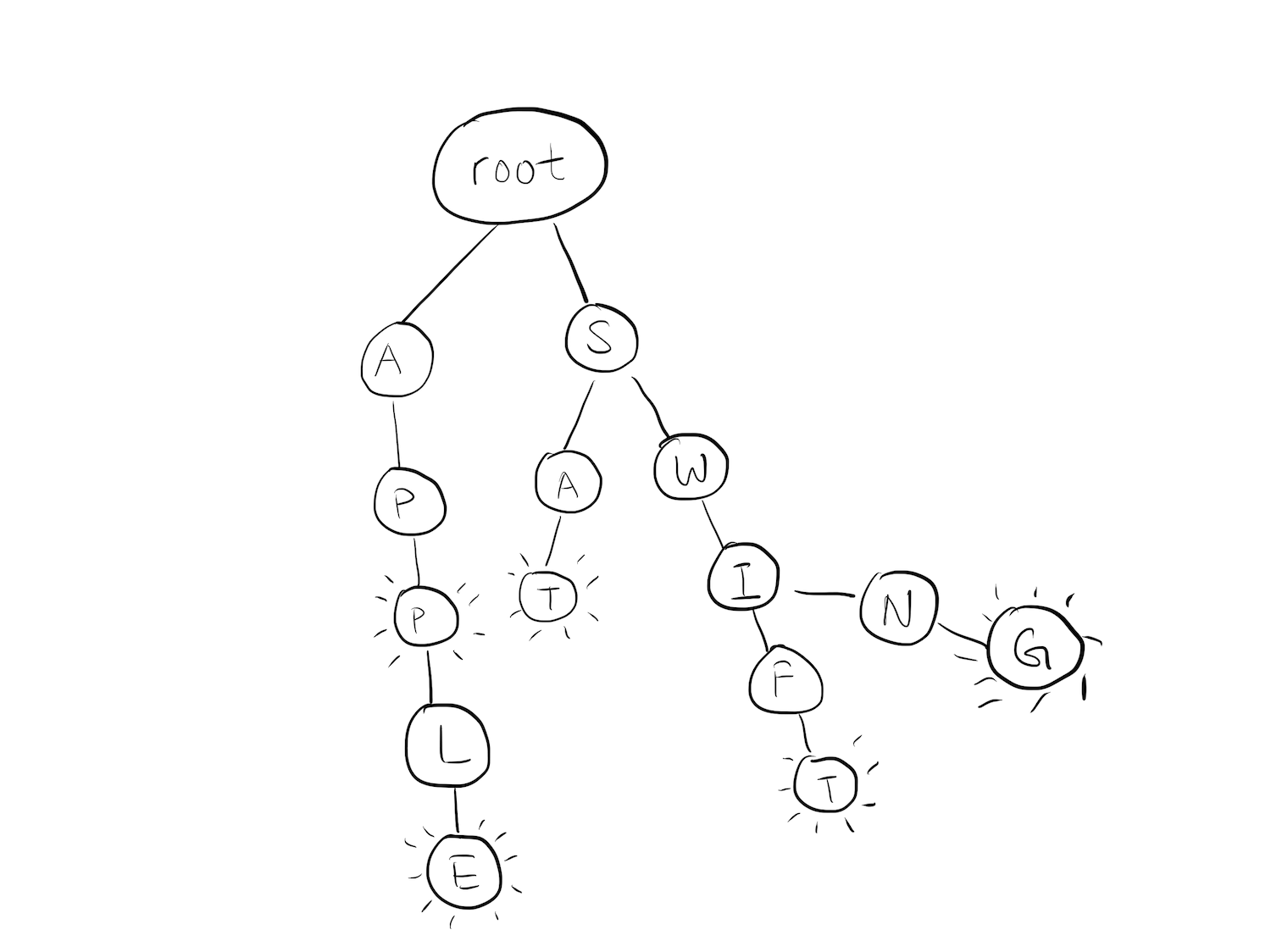
A Trie

存储英语是Trie的主要用处。 Trie中的每个节点都代表一个单词的单个字符。 然后，一系列节点组成一个单词。

为什么需要字典树？

字典树对某些情况非常有用。 以下是一些优点：

  • 查找值通常具有更好的最坏情况时间复杂度。

  • 与哈希映射不同，Trie不需要担心键冲突。

  • 不使用散列来保证元素的唯一路径。

  • Trie结构默认按字母顺序排列。

常用算法

包含（或任何常规查找方法）

Trie结构非常适合查找操作。 对于模拟英语语言的Trie结构，找到一个特定的单词就是几个指针遍历的问题：

func contains(word: String) -> Bool {
	guard !word.isEmpty else { return false }

	// 1
	var currentNode = root
  
	// 2
	var characters = Array(word.lowercased().characters)
	var currentIndex = 0
 
	// 3
	while currentIndex < characters.count, 
	  let child = currentNode.children[characters[currentIndex]] {

	  currentNode = child
	  currentIndex += 1
	}

	// 4
	if currentIndex == characters.count && currentNode.isTerminating {
	  return true
	} else {
	  return false
	}
}

 

contains方法相当简单：

  1. 创建对root的引用。 此引用将允许您沿着节点链向下走。

  2. 跟踪你想要匹配的单词的字符。

  3. 将指针向下移动节点。

  4. isTerminating是一个布尔标志，表示该节点是否是单词的结尾。 如果满足此if条件，则意味着您可以在trie中找到该单词。

插入

插入Trie需要您遍历节点，直到您停止必须标记为terminating的节点，或者到达需要添加额外节点的点。

func insert(word: String) {
  guard !word.isEmpty else {
    return
  }

  // 1
  var currentNode = root

  // 2
  for character in word.lowercased().characters {
    // 3
    if let childNode = currentNode.children[character] {
      currentNode = childNode
    } else {
      currentNode.add(value: character)
      currentNode = currentNode.children[character]!
    }
  }
  // Word already present?
  guard !currentNode.isTerminating else {
    return
  }

  // 4
  wordCount += 1
  currentNode.isTerminating = true
}

  1. 再次，您创建对根节点的引用。 您将此引用沿着节点链移动。

  2. 逐字逐句地逐字逐句

  3. 有时，要插入的节点已存在。 这是Trie里面两个共享字母的词（即“Apple”，“App”）。如果一个字母已经存在，你将重复使用它，并简单地遍历链条。 否则，您将创建一个表示该字母的新节点。

  4. 一旦结束，将isTerminating标记为true，将该特定节点标记为单词的结尾。

删除

从字典树中删除键有点棘手，因为还有一些情况需要考虑。 Trie中的节点可以在不同的单词之间共享。 考虑两个词“Apple”和“App”。 在Trie中，代表“App”的节点链与“Apple”共享。

如果你想删除“Apple”，你需要注意保持“App”链。

func remove(word: String) {
  guard !word.isEmpty else {
    return
  }

  // 1
  guard let terminalNode = findTerminalNodeOf(word: word) else {
    return
  }

  // 2
  if terminalNode.isLeaf {
    deleteNodesForWordEndingWith(terminalNode: terminalNode)
  } else {
    terminalNode.isTerminating = false
  }
  wordCount -= 1
}

 

  1. findTerminalNodeOf遍历字典树，找到代表word的最后一个节点。 如果它无法遍历字符串，则返回nil。

  2. deleteNodesForWordEndingWith遍历后缀，删除word表示的节点。

 

时间复杂度

设n是Trie中某个值的长度。

  • contains - 最差情况O(n)

  • insert - O(n)

  • remove - O(n)

其他值得注意的操作

  • count：返回Trie中的键数 —— O(1)

  • words：返回包含Trie中所有键的列表 —— O(1)

  • isEmpty：如果Trie为空则返回true，否则返回false —— O(1)

扩展阅读字典树的维基百科

B树（B-Tree）

A B-Tree is a self-balancing search tree, in which nodes can have more than two children.
B-Tree是一种自平衡搜索树，其中节点可以有两个以上的子节点。

Properties

性质

A B-Tree of order n satisfies the following properties:

  • Every node has at most 2n keys.

  • Every node (except root) has at least n keys.

  • Every non-leaf node with k keys has k+1 children.

  • The keys in all nodes are sorted in increasing order.

  • The subtree between two keys k and l of a non-leaf node contains all the keys between k and l.

  • All leaves appear at the same level.

B树排序满足以下性质：
  - 每个节点最多有 2n 个键。
  - 每个节点（root除外）至少有 n 个键。
  - 每个带有 k 个键的非叶节点都有 k+1 个子节点。
  - 所有节点中的键按递增顺序排序。
  - 非叶节点的两个键 k 和 l 之间的子树包含 k 和 l 之间的所有键。
  - 所有叶节点出现在同一水平。

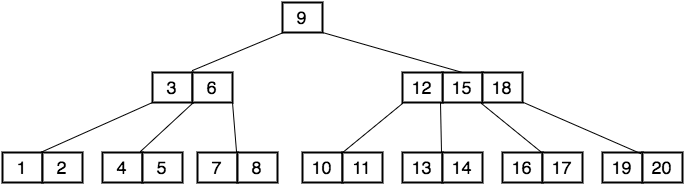
A second order B-Tree with keys from 1 to 20 looks like this:
带有1到20键的二阶B-Tree看起来像这样：

A B-Tree with 20 keys.

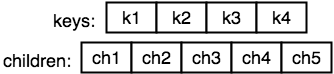
The representation of a B-Tree node in code

代码中B树节点的表示

class BTreeNode<Key: Comparable, Value> {
  unowned var owner: BTree<Key, Value>
  
  fileprivate var keys = [Key]()
  var children: [BTreeNode]?
  
  ...
}

The main parts of a node are two arrays:

  • An array containing the keys

  • An array containing the children

节点的主要部分是两个数组属性：
  - 包含键的数组
  - 包含子项的数组

Node.

Nodes also have a reference to the tree they belong to.
This is necessary because nodes have to know the order of the tree.

节点还引用了它们所属的树。
这是必要的，因为节点必须知道树的排序。

Note: The array containing the children is an Optional, because leaf nodes don't have children.
注意：包含子节点的数组是可选的，因为叶节点没有子节点。

Searching

搜索

  1. Searching for a key k begins at the root node.

  2. We perform a linear search on the keys of the node, until we find a key l that is not less than k,
    or reach the end of the array.

  3. If k == l then we have found the key.

  4. If k < l:

    • If the node we are on is not a leaf, then we go to the left child of l, and perform the steps 3 - 5 again.

    • If we are on a leaf, then k is not in the tree.

  5. If we have reached the end of the array:

    • If we are on a non-leaf node, then we go to the last child of the node, and perform the steps 3 - 5 again.

    • If we are on a leaf, then k is not in the tree.

  6. 从根节点开始搜索键k。

  7. 我们对节点的键进行线性搜索，直到找到一个不小于k的键l，或到达数组的末尾。

  8. 如果k == l那么我们找到了键。

  9. 如果k <l：
         - 如果我们所在的节点不是叶节点，那么我们转到l的左子节点，然后再次执行步骤3 - 5。
         - 如果我们在叶子节点，那么k不在树上。

  10. 如果我们到达了数组的末尾：
         - 如果我们在非叶节点上，那么我们转到节点的最后一个子节点，然后再次执行步骤3 - 5。
         - 如果我们在叶子上，那么k不在树上。

代码

 

value(for:) method searches for the given key and if it's in the tree,
it returns the value associated with it, else it returns nil.
value(for:)方法搜索给定的键，如果它在树中，它返回与之关联的值，否则返回nil。

Insertion

插入

Keys can only be inserted to leaf nodes.
键只能插入叶节点。

  1. Perform a search for the key k we want to insert.

  2. If we haven't found it and we are on a leaf node, we can insert it.

  • If after the search the key l which we are standing on is greater than k:
    We insert k to the position before l.

  • Else:
    We insert k to the position after l.

  1. 搜索我们要插入的键k。

  2. 如果我们没有找到它并且我们在叶节点上，我们可以插入它。
      - 如果在搜索之后我们所在的键l大于k：
        我们在l之前插入k。
      - 否则：
        我们在l之后插入k。

After insertion we should check if the number of keys in the node is in the correct range.
If there are more keys in the node than order*2, we need to split the node.
插入后，我们应检查节点中的键数是否在正确的范围内。如果节点中的键多于order * 2，我们需要拆分节点。

Splitting a node

拆分节点

  1. Move up the middle key of the node we want to split, to its parent (if it has one).

  2. If it hasn't got a parent(it is the root), then create a new root and insert to it.
    Also add the old root as the left child of the new root.

  3. Split the node into two by moving the keys (and children, if it's a non-leaf) that were after the middle key
    to a new node.

  4. Add the new node as a right child for the key that we have moved up.

  5. 将我们要拆分的节点的中间键向上移动到其父节点（如果有的话）。

  6. 如果它没有父（它是根节点），则创建一个新根节点并插入它。还要将旧根节点添加为新根节点的左子节点。

  7. 通过移动中间键之后的键（以及子项，如果它是非叶子）将节点拆分为两个到一个新节点。

  8. 将新节点添加为我们向上移动的键的右子节点。

After splitting a node it is possible that the parent node will also contain too many keys, so we need to split it also.
In the worst case the splitting goes up to the root (in this case the height of the tree increases).
拆分节点后，父节点可能也包含太多的键，因此我们也需要拆分它。
在最坏的情况下，分裂上升到根（在这种情况下，树的高度增加）。

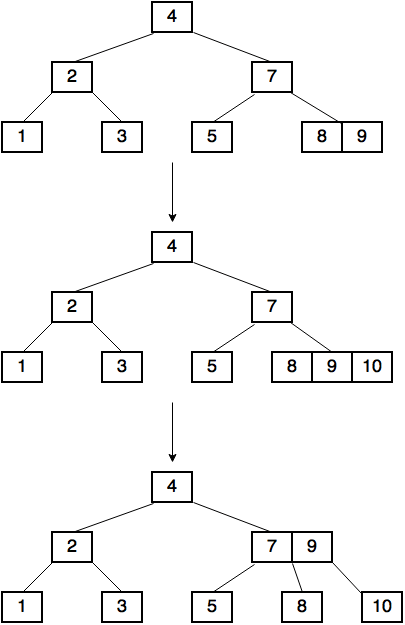
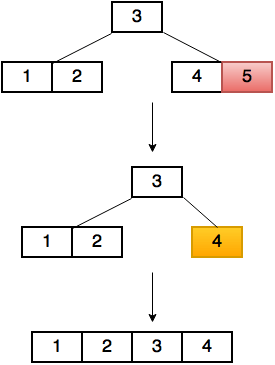
An insertion to a first order tree looks like this:
对第一个顺序树的插入如下所示：

Splitting

The code

The method insert(_:for:) does the insertion.
After it has inserted a key, as the recursion goes up every node checks the number of keys in its child.
if a node has too many keys, its parent calls the split(child:atIndex:) method on it.
方法 insert(_:for:) 进行插入。
插入键后，随着递归的增加，每个节点都会检查其子节点中的键数。
如果一个节点有太多的键，它的父节点就会调用 split(child:atIndex:) 方法。

The root node is checked by the tree itself.
If the root has too many nodes after the insertion the tree calls the splitRoot() method.
根节点由树本身检查。
如果插入后根有太多节点，则树会调用splitRoot()方法。

Removal

删除

Keys can only be removed from leaf nodes.

  1. Perform a search for the key k we want to remove.

  2. If we have found it:

    • If we are on a leaf node:
      We can remove the key.

    • Else:
      We overwrite k with its inorder predecessor p, then we remove p from the leaf node.

只能从叶节点中删除键。

1.搜索我们要删除的键k。
2.如果我们找到了它：
    - 如果我们在叶子节点上：
      我们可以删除键。
    - 否则：
      我们用它的前驱节点p覆盖k，然后我们从叶节点中删除p。

After a key have been removed from a node we should check that the node has enough keys.
If a node has fewer keys than the order of the tree, then we should move a key to it,
or merge it with one of its siblings.
从节点中删除键后，我们应该检查节点是否有足够的键。如果一个节点的键少于树的规定，那么我们应该移动一个键，或者与其中一个兄弟节点合并。

Moving a key to the child

将键移给子节点

If the problematic node has a nearest sibling that has more keys than the order of the tree,
we should perform this operation on the tree, else we should merge the node with one of its siblings.
如果有问题的节点具有最近的兄弟节点，其具有比树规定的更多的键，我们应该在树上执行此操作，否则我们应该将节点与其中一个兄弟节点合并。

Let's say the child we want to fix c1 is at index i in its parent node's children array.
假设我们要修复c1的子节点在其父节点的children数组中的索引i。

If the child c2 at index i-1 has more keys than the order of the tree:
如果索引i-1中的子节点c2的键数多于树的规定：

  1. We move the key at index i-1 from the parent node to the child c1's keys array at index 0.

  2. We move the last key from c2 to the parent's keys array at index i-1.

  3. (If c1 is non-leaf) We move the last child from c2 to c1's children array at index 0.

  4. 我们将索引i-1的键从父节点移动到索引为0的子节点c1的keys数组。

  5. 我们将最后一个键从c2移动到索引i-1的父键数组。

  6. （如果c1是非叶节点）我们将最后一个子节点从c2移动到c1的子数组，在索引0处。

Else:

  1. We move the key at index i from the parent node to the end of child c1's keys array.

  2. We move the first key from c2 to the parent's keys array at index i.

  3. (If c1 isn't a leaf) We move the first child from c2 to the end of c1's children array.

另外：

  1. 我们将索引i的键从父节点移动到子节点c1的keys数组的末尾。

  2. 我们将第一个键从c2移动到索引i的父keys数组。

  3. （如果c1不是叶几点）我们将第一个子节点从c2移动到c1的children数组的末尾。

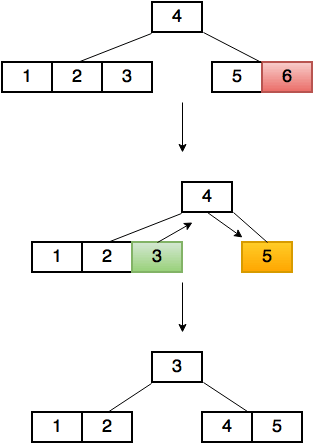
Moving Key

Merging two nodes

合并两个节点

Let's say we want to merge the child c1 at index i in its parent's children array.
假设我们想要在父节点的子数组中将索引i处的子节点c1合并。

If c1 has a left sibling c2:
如果c1有一个左兄弟节点c2：

  1. We move the key from the parent at index i-1 to the end of c2's keys array.

  2. We move the keys and the children(if it's a non-leaf) from c1 to the end of c2's keys and children array.

  3. We remove the child at index i-1 from the parent node.

  4. 我们将密钥从索引“i-1”的父级移动到“c2”的密钥数组的末尾。

  5. 我们将键和子项（如果它是非叶子）从c1移动到c2的键和子数组的末尾。

  6. 我们从父节点删除索引“i-1”的子节点。

Else if c1 only has a right sibling c2:
否则，如果c1只有一个右兄弟节点c2：

  1. We move the key from the parent at index i to the beginning of c2's keys array.

  2. We move the keys and the children(if it's a non-leaf) from c1 to the beginning of c2's keys and children array.

  3. We remove the child at index i from the parent node.

  4. 我们将键从索引i的父节点移动到c2的keys数组的开头。

  5. 我们将键和子节点（如果它是非叶节点）从c1移动到c2的keys和children数组的开头。

  6. 我们从父节点删除索引i处的子节点。

After merging it is possible that now the parent node contains too few keys,
so in the worst case merging also can go up to the root, in which case the height of the tree decreases.
合并后，现在父节点可能包含太少的键，所以在最坏的情况下，合并也可以到达根，在这种情况下，树的高度会降低。

Merging Nodes

代码

  • remove(_:) method removes the given key from the tree. After a key has been deleted,
    every node checks the number of keys in its child. If a child has less nodes than the order of the tree,
    it calls the fix(childWithTooFewKeys:atIndex:) method.

  • fix(childWithTooFewKeys:atIndex:) method decides which way to fix the child (by moving a key to it,
    or by merging it), then calls move(keyAtIndex:to:from:at:) or
    merge(child:atIndex:to:) method according to its choice.

 

  • remove(_:)方法从树中删除给定的键。 删除键后，每个节点都会检查其子节点中的键数。 如果子树中节点数少于树的规定，
       它调用fix(childWithTooFewKeys:atIndex:) 方法。

  • fix(childWithTooFewKeys:atIndex:)方法可以修复子节点的方法（通过移动一个键，或者通过合并它），然后根据选择调用move(keyAtIndex:to:from:at:)或 fix(childWithTooFewKeys:atIndex:) 。

扩展阅读

 

B树维基百科
GeeksforGeeks

下一篇:Swift算法俱乐部

Made with ♥ in Shangrao,China By 老雷

Copyright © devler.cn 1987 - Present

赣ICP备19009883号-1
网站地图 联系我们 隐私政策 用户协议