杂项

• *搅乱算法－随机搅乱数组中的内容。

• *梳排序 - 基于冒泡算法后提高的算法

• *凸包算法

• *米勒-拉宾素性测试 这是一个素数吗？

• *换硬币数量最小问题 一个动态规划的例子

Shuffle

洗牌算法

Goal: Rearrange the contents of an array.
目标：重新排列数组的内容。

Imagine you're making a card game and you need to shuffle a deck of cards. You can represent the deck by an array of Card objects and shuffling the deck means to change the order of those objects in the array. (It's like the opposite of sorting.)

想象一下，你正在进行纸牌游戏，你需要洗牌。 您可以通过一组“卡片”对象来表示卡片组，并对卡片组件进行洗牌，以更改阵列中这些对象的顺序。 （这与排序相反。）

Here is a naive way to approach this in Swift:
这是在Swift中解决这个问题的一种原始的方式：

extension Array {
  public mutating func shuffle() {
    var temp = [Element]()
    while !isEmpty {
      let i = random(count)
      let obj = remove(at: i)
      temp.append(obj)
    }
    self = temp
  }
}

To try it out, copy the code into a playground and then do:
要试用它，将代码复制到playground然后执行：

var list = [ "a", "b", "c", "d", "e", "f", "g" ]
list.shuffle()
list.shuffle()
list.shuffle()

You should see three different arrangements -- or permutations to use math-speak -- of the objects in the array.
您应该看到三种不同的排列 - 或排列来使用数学说话 - 数组中的对象。

This shuffle works in place, it modifies the contents of the original array. The algorithm works by creating a new array, temp, that is initially empty. Then we randomly choose an element from the original array and append it to temp, until the original array is empty. Finally, the temporary array is copied back into the original one.
这个shuffle 就位，它修改了原始数组的内容。 该算法通过创建一个最初为空的新数组temp来工作。 然后我们从原始数组中随机选择一个元素并将其附加到temp，直到原始数组为空。 最后，将临时数组复制回原始数组。

This code works just fine but it's not very efficient. Removing an element from an array is an O(n) operation and we perform this n times, making the total algorithm O(n²⁾. We can do better!
这段代码工作得很好，但效率不高。 从数组中删除元素是一个O(n)操作，我们执行** n 次，使总算法 **O(n2)。 我们可以做得更好！

The Fisher-Yates / Knuth shuffle

Here is a much improved version of the shuffle algorithm:
这是一个改进版本的洗牌算法：

extension Array {
  public mutating func shuffle() {
    for i in stride(from: count - 1, through: 1, by: -1) {
      let j = Int.random(in: 0...i)
      if i != j {
        swap(&self[i], &self[j])
      }
    }
  }
}

Again, this picks objects at random. In the naive version we placed those objects into a new temporary array so we could keep track of which objects were already shuffled and which still remained to be done. In this improved algorithm, however, we'll move the shuffled objects to the end of the original array.
同样，这会随机选择对象。 在天真的版本中，我们将这些对象放入一个新的临时数组中，这样我们就可以跟踪哪些对象已经被洗牌，哪些仍然有待完成。 但是，在这个改进的算法中，我们将混洗的对象移动到原始数组的末尾。

Let's walk through the example. We have the array:
让我们来看看这个例子。 我们有数组：

[ "a", "b", "c", "d", "e", "f", "g" ]

The loop starts at the end of the array and works its way back to the beginning. The very first random number can be any element from the entire array. Let's say it returns 2, the index of "c". We swap "c" with "g" to move it to the end:
循环从数组的末尾开始，然后返回到开头。 第一个随机数可以是整个数组中的任何元素。 假设它返回2，即"c"的索引。 我们将"c"与"g"交换到最后：

[ "a", "b", "g", "d", "e", "f" | "c" ]
* *

The array now consists of two regions, indicated by the | bar. Everything to the right of the bar is shuffled already.
该数组现在由两个区域组成，由|条表示。 酒吧右边的所有东西都已经洗牌了。

The next random number is chosen from the range 0...6, so only from the region [ "a", "b", "g", "d", "e", "f" ]. It will never choose "c" since that object is done and we'll no longer touch it.
下一个随机数是从0...6的范围中选择的，所以只能从区域[ "a", "b", "g", "d", "e", "f" ]中选择。它永远不会选择"c"，因为该对象已完成，我们将不再触摸它。

Let's say the random number generator picks 0, the index of "a". Then we swap "a" with "f", which is the last element in the unshuffled portion, and the array looks like this:
假设随机数生成器选择0，即"a"的索引。 然后我们将"a"与"f"交换，这是未洗过的部分中的最后一个元素，数组如下所示：

[ "f", "b", "g", "d", "e" | "a", "c" ]
* *

The next random number is somewhere in [ "f", "b", "g", "d", "e" ], so let's say it is 3. We swap "d" with "e":
下一个随机数在某个地方[ "f", "b", "g", "d", "e" ]，所以我们说它是3.我们将"d"与"e"交换：

[ "f", "b", "g", "e" | "d", "a", "c" ]
* *

And so on... This continues until there is only one element remaining in the left portion. For example:
等等......这一直持续到左侧部分只剩下一个元素。 例如：

[ "b" | "e", "f", "g", "d", "a", "c" ]

There's nothing left to swap that "b" with, so we're done.
没有什么可以交换"b"了，所以我们已经完成了。

Because we only look at each array element once, this algorithm has a guaranteed running time of O(n). It's as fast as you could hope to get!
因为我们只查看每个数组元素一次，所以该算法的运行时间保证为 O(n)。 它的速度和你希望的一样快！

Creating a new array that is shuffled

创建一个被洗牌的新数组

There is a slight variation on this algorithm that is useful for when you want to create a new array instance that contains the values 0 to n-1 in random order.
当您想要以随机顺序创建包含值0到n-1的新数组实例时，此算法略有不同。

Here is the code:

public func shuffledArray(_ n: Int) -> [Int] {
  var a = [Int](repeating: 0, count: n)
  for i in 0..<n {
    let j = Int.random(in: 0...i)
    if i != j {
      a[i] = a[j]
    }
    a[j] = i
  }
  return a
}

To use it:

let numbers = shuffledArray(10)

This returns something like [3, 0, 9, 1, 8, 5, 2, 6, 7, 4]. As you can see, every number between 0 and 10 is in that list, but shuffled around. Of course, when you try it for yourself the order of the numbers will be different.
这会返回类似[3, 0, 9, 1, 8, 5, 2, 6, 7, 4]的内容。 正如您所看到的，0到10之间的每个数字都在该列表中，但随机摆动。 当然，当你自己尝试时，数字的顺序会有所不同。

The shuffledArray() function first creates a new array with n zeros. Then it loops n times and in each step adds the next number from the sequence to a random position in the array. The trick is to make sure that none of these numbers gets overwritten with the next one, so it moves the previous number out of the way first!
shuffledArray()函数首先创建一个带有n零的新数组。 然后它循环n次，并在每个步骤中将序列中的下一个数字添加到数组中的随机位置。 诀窍是确保这些数字都不会被下一个数字覆盖，所以它先将前一个数字移开！

The algoritm is quite clever and I suggest you walk through an example yourself, either on paper or in the playground. (Hint: Again it splits the array into two regions.)
算法很聪明，我建议你自己走一个例子，无论是在纸上还是在操场上。 （提示：再次将数组拆分为两个区域。）

See also

扩展阅读

These Swift implementations are based on pseudocode from the Wikipedia article.
这些Swift实现基于Wikipedia文章中的伪代码。

Mike Bostock has a great visualization of the shuffle algorithm.
Mike Bostock有一个shuffle算法的很好的可视化。

Comb Sort

梳排序

A common issue for Bubble Sort is when small values are located near the end of an array.
This problem severely slows down Bubble Sort, as it must move the small value -- or turtle --
through nearly the entire array. Bubble Sort works by checking the current index of an array
against the next index, and when those two values are unsorted, they are swapped into place.
As a result, the values bubble into their rightful place within the array.

冒泡排序的一个常见问题是当小值位于数组末尾附近时。
这个问题严重减慢了冒泡排序，因为它必须移动小值 - 或 turtle -- 通过几乎整个数组。 冒泡排序的工作原理是检查数组的当前索引对于下一个索引，当这两个值未排序时，它们将被交换到位。结果，这些值冒泡到数组中的合法位置。

Comb Sort improves upon Bubble Sort by dealing with these turtles near the end of the array.
The value of the current index of the array is compared against one a set distance away. This
removes a worst-case scenario of Bubble Sort, and greatly improves on the time complexity of Bubble Sort.
梳排序通过处理数组末端附近的这些turtles来改进冒泡排序。
将数组的当前索引的值与设定距离之一进行比较。 这个消除了冒泡排序的最坏情况，并大大提高了冒泡排序的时间复杂度。

Example

例子

A step-by-step example of how Comb Sort works, and differs from Bubble Sort, can be seen here.
有关梳排序如何工作的分步示例，与冒泡排序不同，可以看这里。

Here is a visual to see Comb Sort in effect:
这是一个视觉效果，可以看到有效的梳子排序：

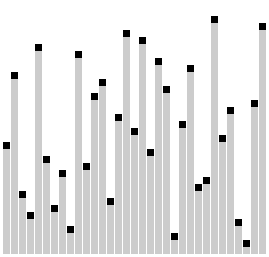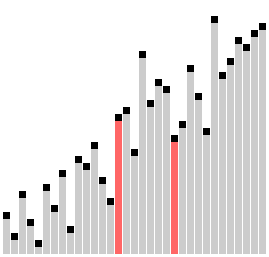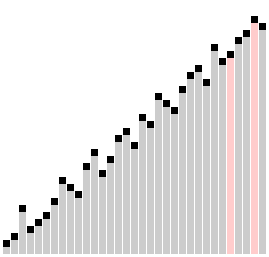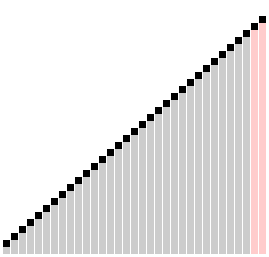
Algorithm

算法

Similar to Bubble Sort, two values within an array are compared. When the lower index value
is larger than the higher index value, and thus out of place within the array, they are
swapped. Unlike Bubble Sort, the value being compared against is a set distance away. This
value -- the gap -- is slowly decreased through iterations.

与冒泡排序类似，比较数组中的两个值。 当指数值较低时它们大于较高的索引值，因此在数组中不合适，它们是交换。 与冒泡排序不同，要比较的值是设定的距离。 这个value - gap - 通过迭代缓慢减少。

The Code

代码

Here is a Swift implementation of Comb Sort:
这是一个Swift实现的梳子排序：

func combSort (input: [Int]) -> [Int] {
    var copy: [Int] = input
    var gap = copy.count
    let shrink = 1.3

    while gap > 1 {
        gap = (Int)(Double(gap) / shrink)
        if gap < 1 {
            gap = 1
        }
    
        var index = 0
        while !(index + gap >= copy.count) {
            if copy[index] > copy[index + gap] {
                swap(&copy[index], &copy[index + gap])
            }
            index += 1
        }
    }
    return copy
}

This code can be tested in a playground by calling this method with a paramaterized array to sort:
可以通过使用参数化数组调用此方法来在playground中测试此代码以进行排序：

combSort(example_array_of_values)

This will sort the values of the array into ascending order -- increasing in value.
这将按照升序对数组的值进行排序 - 增加值。

Performance

性能

Comb Sort was created to improve upon the worst case time complexity of Bubble Sort. With Comb
Sort, the worst case scenario for performance is exponential -- O(n^2). At best though, Comb Sort
performs at O(n logn) time complexity. This creates a drastic improvement over Bubble Sort's performance.

Similar to Bubble Sort, the space complexity for Comb Sort is constant -- O(1).
This is extremely space efficient as it sorts the array in place.

创建梳排序是为了改善冒泡排序的最坏情况时间复杂度。 随着梳子排序，性能的最坏情况是指数 - O(n^2)。 最好的是，梳子排序以O(n logn)时间复杂度执行。 这比冒泡排序的性能产生了巨大的改进。

与冒泡排序类似，梳子排序的空间复杂度是常数 - O(1)。
这是非常节省空间的，因为它对数组进行了原地排序。

Additional Resources

补充资源

梳排序的维基百科

Written for the Swift Algorithm Club by Stephen Rutstein

Convex Hull

凸包

Given a group of points on a plane. The Convex Hull algorithm calculates the shape (made up from the points itself) containing all these points. It can also be used on a collection of points of different dimensions. This implementation however covers points on a plane. It essentially calculates the lines between points which together contain all points. In comparing different solutions to this problem we can describe each algorithm in terms of it's big-O time complexity.

给出平面上的一组点。 凸包算法计算包含所有这些点的形状（由点本身组成）。 它也可以用于不同维度的点集合。 然而，该实现涵盖了平面上的点。 它实质上计算了包含所有点的点之间的线。 在比较这个问题的不同解决方案时，我们可以根据它的大O时间复杂度来描述每个算法。

There are multiple Convex Hull algorithms but this solution is called Quickhull, is comes from the work of both W. Eddy in 1977 and also separately A. Bykat in 1978, this algorithm has an expected time complexity of O(n log n), but it's worst-case time-complexity can be O(n^2) . With average conditions the algorithm has ok efficiency, but it's time-complexity can start to head become more exponential in cases of high symmetry or where there are points lying on the circumference of a circle for example.

有多个凸包算法，一个解决方案叫做Quickhull，它来自于1977年的W. Eddy和1978年的A. Bykat的工作，该算法的预期时间复杂度为O(n log n)，但是 最糟糕的情况是时间复杂度可以是O(n^2)。 在平均条件下，算法具有良好的效率，但是在高对称性的情况下或者例如在圆周上存在点的情况下，时间复杂度可以开始变得更具指数性。

Quickhull

The quickhull algorithm works as follows:

• The algorithm takes an input of a collection of points. These points should be ordered on their x-coordinate value.

• We first find the two points A and B with the minimum(A) and the maximum(B) x-coordinates (as these will obviously be part of the hull).

• Use the line formed by the two points to divide the set in two subsets of points, which will be processed recursively.

• Determine the point, on one side of the line, with the maximum distance from the line. The two points found before along with this one form a triangle.

• The points lying inside of that triangle cannot be part of the convex hull and can therefore be ignored in the next steps.

• Repeat the previous two steps on the two lines formed by the triangle (not the initial line).

• Keep on doing so on until no more points are left, the recursion has come to an end and the points selected constitute the convex hull.

quickhull算法的工作原理如下：

• 算法接受点集合的输入。 这些点应按其x坐标值排序。

• 我们首先找到具有最小（A）和最大（B）x坐标的两个点A和B（因为这些将显然是船体的一部分）。

• 使用由两点组成的直线将集合分成两个点子集，这些点将以递归方式处理。

• 确定线的一侧的点与线的最大距离。 之前发现的两点与此形成一个三角形。

• 位于该三角形内部的点不能是凸包的一部分，因此可以在后续步骤中忽略。

• 在由三角形（而不是初始线）形成的两条线上重复前两步。

• 继续这样做直到没有剩下的点，递归已经结束并且所选择的点构成凸包。

Our functioni will have the following defininition:
我们的功能将具有以下定义：

findHull(points: [CGPoint], p1: CGPoint, p2: CGPoint)

findHull(S1, A, B)
findHull(S2, B, A)

What this function does is the following:

1. If points is empty we return as there are no points to the right of our line to add to our hull.

2. Draw a line from p1 to p2.

3. Find the point in points that is furthest away from this line. (maxPoint)

4. Add maxPoint to the hull right after p1.

5. Draw a line (line1) from p1 to maxPoint.

6. Draw a line (line2) from maxPoint to p2. (These lines now form a triangle)

7. All points within this triangle are of course not part of the hull and thus can be ignored. We check which points in points are to the right of line1 these are grouped in an array s1.

8. All points that are to the right of line2 are grouped in an array s2. Note that there are no points that are both to the right of line1 and line2 as then maxPoint wouldn't be the point furthest away from our initial line between p1 and p2.

9. We call findHull(_, _, _) again on our new groups of points to find more hull points.

这个功能的作用如下：

1. 如果points为空，我们返回，因为我们的线右边没有点添加到我们的船体。

2. 从p1到p2画一条线。

3. 找到离这条线最远的“点”点。（maxPoint）

4. 在p1之后立即将maxPoint添加到船体。

5. 从p1到maxPoint画一条线（line1）。

6. 从maxPoint画一条线（line2）到'p2。 （这些线现在形成一个三角形） 7. 此三角形内的所有点当然不是船体的一部分，因此可以忽略。 我们检查points中哪些点位于line1'的右边，这些点被分组在一个数组s1中。

7. “line2”右边的所有点都分组在一个数组s2中。 注意，在'line1和line2的右边没有任何点，因为maxPoint不会是离'p1和p2之间的初始线最远的点。

8. 我们在新的点组上再次调用findHull（_，_，_）以找到更多的船体点。

findHull(s1, p1, maxPoint)
findHull(s2, maxPoint, p2)

This eventually leaves us with an array of points describing the convex hull.
这最终给我们留下了一系列描述凸包的点。

See also

扩展阅读

凸包的维基百科

Written for the Swift Algorithm Club by Jaap Wijnen.

Miller-Rabin Primality Test

Miller-Rabin素性检测

In 1976, Gray Miller introduced an algorithm, through his ph.d thesis1, which determines a primality of the given number. The original algorithm was deterministic under the Extended Reimann Hypothesis, which is yet to be proven. After four years, Michael O. Rabin improved the algorithm2 by using probabilistic approach and it no longer assumes the unproven hypothesis.

1976年，格雷米勒通过他的博士论文1介绍了一种算法，它确定了给定数字的素数。 原始算法在扩展Reimann假设下是确定性的，尚未得到证实。 四年后，Michael O. Rabin通过使用概率方法改进了算法2，并且不再假设未经证实的假设。

Probabilistic

概率

The result of the test is simply a boolean. However, true does not implicate the number is prime. In fact, it means the number is probably prime. But false does mean the number is composite.
测试结果只是一个布尔值。 但是，true并不意味着 the number is prime 。 事实上，这意味着 the number is probably prime。 但是false的意思是 the number is composite。

In order to increase the accuracy of the test, it needs to be iterated few times. If it returns true in every single iteration, then we can say with confidence that the number is pro......bably prime.
为了提高测试的准确性，需要迭代几次。 如果它在每一次迭代中都返回true，那么我们可以自信地说 the number is pro......bably prime。

Algorithm

算法

Let n be the given number, and write n-1 as 2^s·d, where d is odd. And choose a random number a within the range from 2 to n - 1.
设n为给定数字，并将n-1写为2^s·d，其中d为奇数。 并选择从2到n - 1范围内的随机数a。

Now make a sequence, in modulo n, as following:
现在以模n形式创建一个序列，如下所示：

a^{d, a}(2·d), a^{(4·d), ... , a}((2^{(s-1))·d), a}((2^{s)·d) = a}(n-1)

And we say the number n passes the test, probably prime, if 1) a^d is congruence to 1 in modulo n, or 2) a^((2^k)·d) is congruence to -1 for some k = 1, 2, ..., s-1.
并且我们说数字n通过测试， probably prime ，如果1）a^d与modulon中的1是一致的，或2）a^((2^k)·d) 对于某些 k = 1, 2, ..., s-1，与-1是一致的。

Pseudo Code

伪代码

The following pseudo code is excerpted from Wikipedia3:
以下伪代码摘自维基百科3：

Usage

使用

mrPrimalityTest(7)                      // test if 7 is prime. (default iteration = 1)
mrPrimalityTest(7, iteration: 10)       // test if 7 is prime && iterate 10 times.

Reference

参考

1. G. L. Miller, "Riemann's Hypothesis and Tests for Primality". J. Comput. System Sci. 13 (1976), 300-317.

2. M. O. Rabin, "Probabilistic algorithm for testing primality". Journal of Number Theory. 12 (1980), 128-138.

3. Miller–Rabin primality test - Wikipedia, the free encyclopedia

Written for Swift Algorithm Club by Sahn Cha, @scha00

Minimum Coin Change

最小硬币变换

Minimum Coin Change problem algorithm implemented in Swift comparing dynamic programming algorithm design to traditional greedy approach.
Swift中实现的最小硬币变换问题算法，将动态规划算法设计与传统的贪婪方法进行比较。

Written for Swift Algorithm Club by Jacopo Mangiavacchi

Introduction

介绍

In the traditional coin change problem you have to find all the different ways to change some given money in a particular amount of coins using a given amount of set of coins (i.e. 1 cent, 2 cents, 5 cents, 10 cents etc.).
在传统的硬币更换问题中，您必须找到使用给定数量的硬币（即1美分，2美分，5美分，10美分等）以特定数量的硬币更改某些给定金钱的所有不同方法。

For example using Euro cents the total of 4 cents value of money can be changed in these possible ways:
例如，使用欧元美分，可以通过以下方式更改总共4美分的货币价值：

• Four 1 cent coins

• Two 2 cent coins

• One 2 cent coin and two 1 cent coins
  

• 四个1美分硬币

• 两个2美分硬币

• 一个2美分硬币和两个1美分硬币

The minimum coin change problem is a variation of the generic coin change problem where you need to find the best option for changing the money returning the less number of coins.
最小的硬币变化问题是一般硬币变化问题的变化，你需要找到最好的选项来更换返还少量硬币的钱。

For example using Euro cents the best possible change for 4 cents are two 2 cent coins with a total of two coins.
例如，使用欧元美分，4美分的最佳可能变化是两个2美分硬币，总共两个硬币。

Greedy Solution

贪心解决方案

A simple approach for implementing the Minimum Coin Change algorithm in a very efficient way is to start subtracting from the input value the greater possible coin value from the given amount of set of coins available and iterate subtracting the next greater possible coin value on the resulting difference.
以非常有效的方式实现最小硬币变换算法的一种简单方法是从输入值中减去可用硬币的给定量的硬币值，并迭代减去下一个更大的硬币值。

For example from the total of 4 Euro cents of the example above you can subtract initially 2 cents as the other biggest coins value (from 5 cents to above) are to bigger for the current 4 Euro cent value. Once used the first 2 cents coin you iterate again with the same logic for the rest of 2 cents and select another 2 cents coin and finally return the two 2 cents coins as the best change.
例如，从上面示例的总共4欧分，您可以减去最初的2美分，因为其他最大的硬币值（从5美分到以上）对于当前的4欧分值来说要大一些。一旦使用前2美分硬币，你再次使用相同的逻辑迭代2美分的剩余部分并选择另一个2美分硬币，最后返回两个2美分硬币作为最佳变化。

Most of the time the result for this greedy approach is optimal but for some set of coins the result will not be the optimal.
大多数情况下，这种贪婪方法的结果是最佳的，但对于某些硬币组，结果将不是最佳的。

Indeed, if we use the a set of these three different coins set with values 1, 3 and 4 and execute this greedy algorithm for asking the best change for the value 6 we will get one coin of 4 and two coins of 1 instead of two coins of 3.
实际上，如果我们使用设置为值1,3和4的这三个不同硬币的一组并执行这个贪婪算法来询问值6的最佳变化，我们将得到一个4硬币和两个硬币1而不是2 硬币3。

Dynamic Programming Solution

动态编程解决方案

A classic dynamic programming strategy will iterate selecting in order a possible coin from the given amount of set of coins and finding using recursive calls the minimum coin change on the difference from the passed value and the selected coin. For any interaction the algorithm select from all possible combinations the one with the less number of coins used.
经典的动态编程策略将迭代选择从给定数量的硬币组中的可能硬币，并使用递归调用找到与传递值和所选硬币的差异的最小硬币变化。对于任何交互，算法从所有可能的组合中选择具有较少数量的硬币的组合。

The dynamic programming approach will always select the optimal change but it will require a number of steps that is at least quadratic in the goal amount to change.
动态编程方法将始终选择最佳变化，但是需要多个步骤，这些步骤至少是要改变的目标量的二次方。

In this Swift implementation in order to optimize the overall performance we use an internal data structure for caching the result for best minimum coin change for previous values.
在此Swift实现中，为了优化整体性能，我们使用内部数据结构来缓存结果，以便为先前的值进行最佳的最小硬币更改。